Калькулятор расчета деревянных балок перекрытия и стропильной системы!
Как пользоваться онлайн калькулятором расчета балок перекрытия и стропил
Чтобы правильно произвести прочностной расчет балки перекрытия и подобрать необходимый тип двутавровой балки, вы можете воспользоваться онлайн-калькулятором. На основе полученных вычислений можно точно рассчитать количество, необходимое для устройства стропильной системы или укладки лаг. Расчет деревянных балок перекрытия возможен только после того, как будет известно расстояние между стенами (расчетная длина балки). Кроме того, необходимо знание величины предполагаемой нагрузки на всю конструкцию.
Для межэтажных перекрытий, в том числе цокольного, используйте значение 400 кг/м2; для чердачного — 200 кг/м2 (или 250 кг/м2, если нагрузка от стропильной системы передается непосредственно на чердачное перекрытие). Для стропильной системы 220 кг/м2 для Московского региона, для других регионов принимайте значения в зависимости от снегового района.
Заказать бесплатный расчет балок по проекту или проконсультироваться у специалистов нашей компании можно по телефону +7(495)105-91-63
+7(812)425-65-03
+7(843)207-04-92
+7(4722)77-73-16
+7(800)333-79-86
+7(421)240-08-29
+7(818)246-42-27
+7(861)212-30-63
+7(800)333-37-59
Так же Вы можете прислать чертежи для расчета на [email protected]
Онлайн калькулятор расчета деревянных балок перекрытия и стропил
Где используются балки
ПерекрытиеСтропила
Вам необходимо выбрать конструкцию, для которой вы будете использовать балки: будет ли это расчет перекрытий (применяются в качестве лаг) или стропильной системы (используются в качестве стропил).
Компания «ИнтерСити» производит износоустойчивые деревянные двутавры. Благодаря отличным эксплуатационным свойствам, изделия могут использоваться в различных конструкциях. Однако нужно помнить, что самостоятельно производить расчет балки перекрытия «на глаз» не следует. Ошибка может привести к прогибу конструкции под нагрузкой и, как следствие, потере возможности дальнейшей эксплуатации.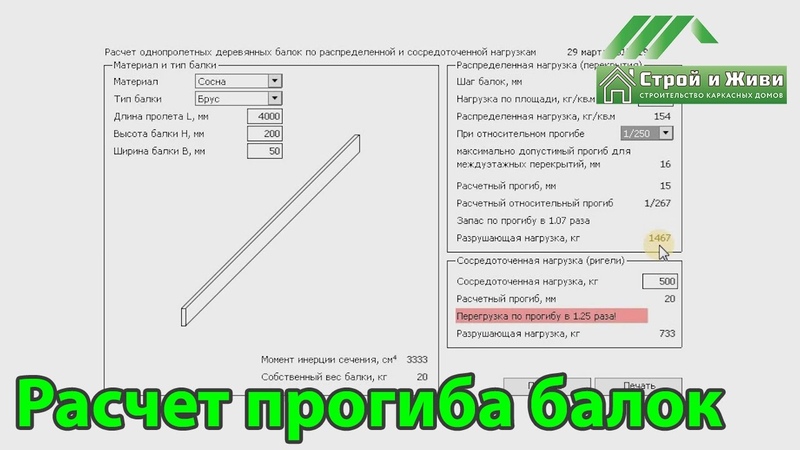
Расчет деревянных балок перекрытий: онлайн калькулятор
Деревянные брусья для перекрытий в частном строительстве используют часто. Легкость, доступность по цене и возможность самостоятельного монтажа компенсируют способность к возгоранию, поражению грибком и гниению. В любом случае при возведению второго и более этажей просто необходимо произвести расчет деревянных балок перекрытия. Онлайн-калькулятор, который мы представляем в этом обзоре, поможет справиться с этой задачей просто и быстро.
Деревянные брусья для перекрытия – только качественная древесинаЧитайте в статье
Польза онлайн-калькулятора для расчета деревянных перекрытий
Самостоятельные расчеты утомительны и чреваты риском не учесть какой-либо важный параметр. Так, деревянные балки для перекрытий должны обладать определенным сечением, учитывающим возможную нагрузку на них от мебели и техники, находящихся в помещении людей. При таких расчетах крайне важно знать возможный прогиб балки и максимальное напряжение в опасном сечении.
Так, деревянные балки для перекрытий должны обладать определенным сечением, учитывающим возможную нагрузку на них от мебели и техники, находящихся в помещении людей. При таких расчетах крайне важно знать возможный прогиб балки и максимальное напряжение в опасном сечении.
Преимущества калькулятора в следующем:
- Точность. Формулы расчета учитывают множество параметров. В специальных полях задаются: тип поперечного сечения (круглое или прямоугольное), длину балки между опорами и шаг, параметры используемой древесины, предполагаемую постоянную нагрузку.
- Сроки. Ввести готовые параметры и получить результат выйдет значительно быстрее, чем рассчитывать вручную требуемые значения.
- Удобство. Онлайн-калькулятор расчета деревянных балок составлен таким образом, что после введения всех постоянных величин, вам остается просто подбирать сечение балки до тех пор, пока не будет обеспечена необходимая прочность.

Расчет деревянного бруса для перекрытия: на что обратить внимание
До расчетов и покупки рекомендовано обратить внимание на типы перекрытий. Брус для надежной связки строительных конструкций, бывает следующих видов:
- Балки. Массив квадратного или прямоугольного сечения, уложенный с шагом от 60 см до 1 м. Стандартная длина – 6 м, на заказ изготавливаются балки до 15 м.
- Ребра. Балки, напоминающие широкую (20 см) и толстую доску (7 см). Шаг укладки на ребро не более 60 см. Стандартная длина – 5 м, под заказ – 12 м.
- Комбинация двух типов бруса. Наиболее надежные перекрытия, служащие опорой для пролетов, до 15 м.
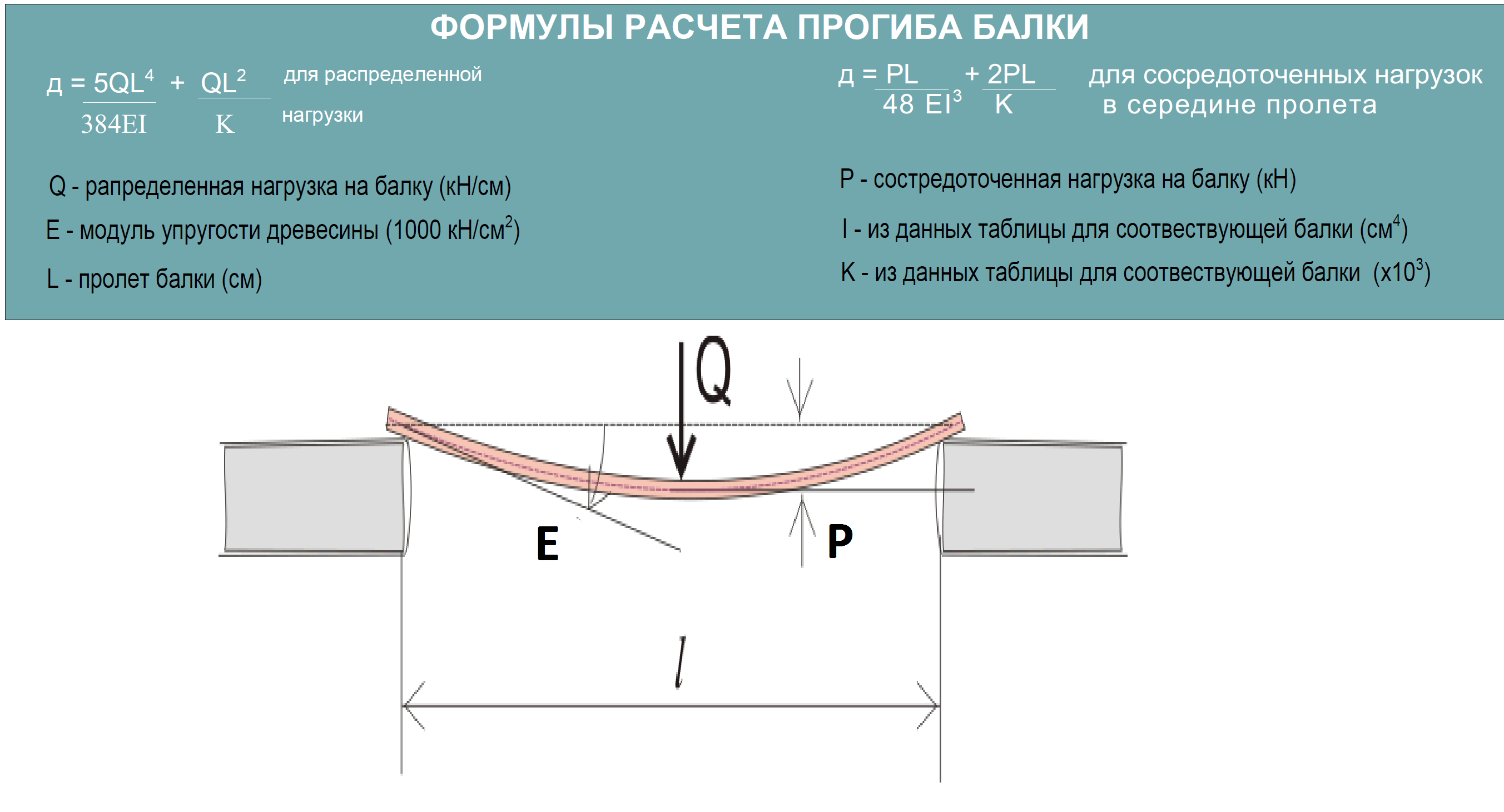
Сначала определяется прогиб балки, максимальное напряжение в опасном сечении и коэффициент запаса прочности. Если значение коэффициента получается меньше 1, то это значит, что прочность не обеспечена. В этом случае необходимо изменить условия расчета (изменить сечение балки, увеличить или уменьшить шаг, выбрать другую породу древесины и т. д.)
д.)
| Длина балок, м | ||||
| Шаг укладки, м | 2,0 | 3,0 | 4,0 | 5,0 |
| 0,6 | 75*100 | 75*200 | 100*200 | 150*225 |
| 1 | 75*150 | 100*175 | 150*200 | 175*250 |
Когда нужное сечение найдено требуется рассчитать его кубатуру. Это произведение длины, ширины и высоты. Далее по проекту находим количество балок перекрытия и умножаем на полученный результат.
Брус
Итог
Сращивание двух балок перекрытия = снижение надежностиВажно! Для строительства многоэтажных домов не рекомендовано приобретать балки недостаточной длины. Сращивание, даже качественное, снижает надежность конструкций.
Для наглядности пользователю предоставлено видео расчета древесины для перекрытий.
ПОНРАВИЛАСЬ СТАТЬЯ? Поддержите нас и поделитесь с друзьями
Расчет деревянной балки Онлайн, расчет несущей способности и прогиба деревянных балок
Распределенная нагрузка (перекрытия)
Шаг балок,мм
Нагрузка по площади, кг/кв.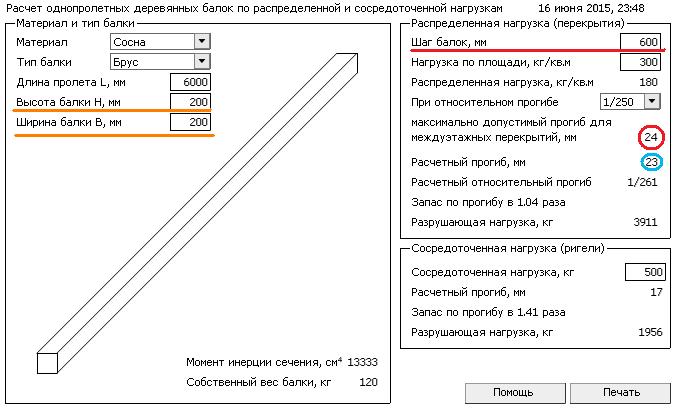 м
м
При относительном прогибе 1/2501/2001/150
максимально допустимый прогиб для междуэтажных перекрытий, мм 16
Расчетный прогиб, мм 12
Расчетный относительный прогиб 1/333
Запас по прогибу в 1.33 раза
Разрушающая нагрузка, кг 2475
Сосредоточенная нагрузка (ригели)
Сосредоточенная нагрузка, кг
Расчетный прогиб, мм 16
Запас по прогибу в 1.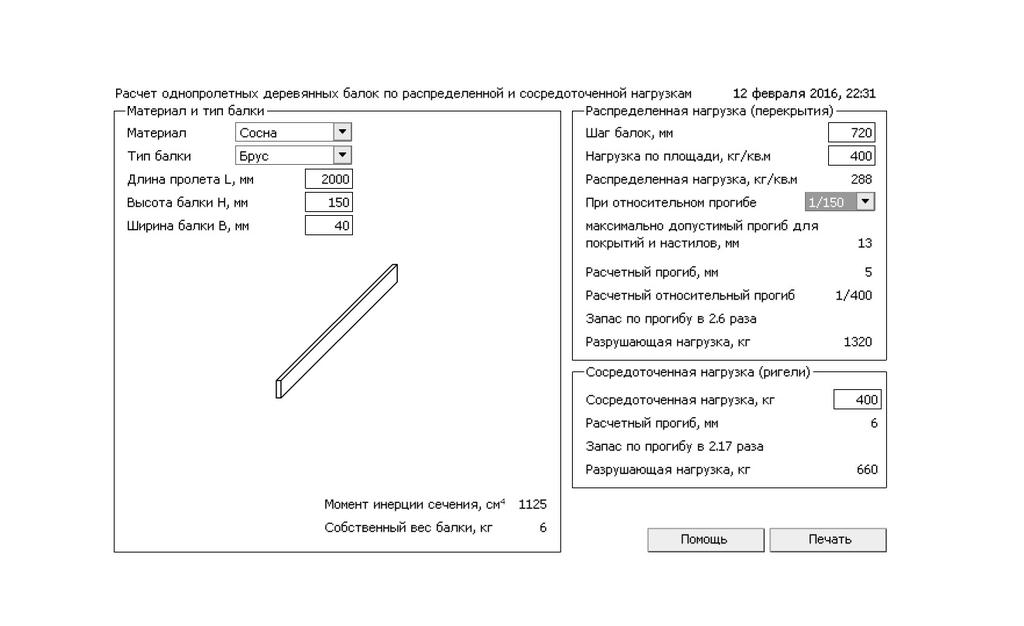 33 раза
33 раза
Разрушающая нагрузка, кг 1238
Расчет несущей способности и прогиба деревянных балок
Чтобы построить деревянный дом необходимо провести расчёт несущей способности деревянной балки. Также особое значение в строительной терминологии имеет определение прогиба.
Без качественного математического анализа всех параметров просто невозможно построить дом из бруса. Именно поэтому перед тем как начать строительство крайне важно правильно рассчитать прогиб деревянных балок. Данные расчёты послужат залогом вашей уверенности в качестве и надёжности постройки.
Что нужно для того чтобы сделать правильный расчёт
Расчёт несущей способности и прогиба деревянных балок не такая простая задача, как может показаться на первый взгляд.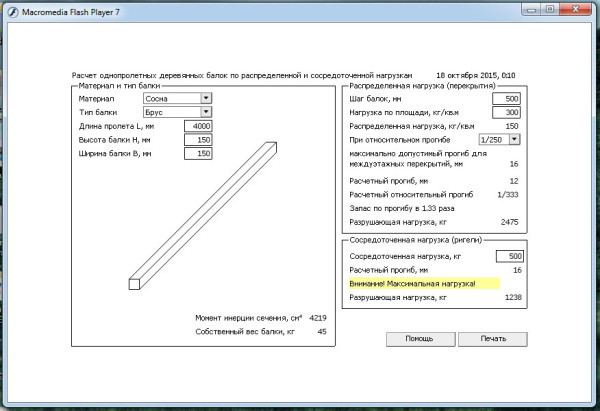 Чтобы определить, сколько досок вам нужно, а также, какой у них должен быть размер необходимо потратить немало времени, или же вы просто можете воспользоваться нашим калькулятором.
Чтобы определить, сколько досок вам нужно, а также, какой у них должен быть размер необходимо потратить немало времени, или же вы просто можете воспользоваться нашим калькулятором.
Во-первых, нужно замерить пролёт, который вы собираетесь перекрыть деревянными балками. Во-вторых, уделите повышенное внимание методу крепления. Крайне важно, насколько глубоко фиксирующие элементы будут заходить в стену. Только после этого вы сможете сделать расчёт несущей способности вместе с прогибом и ряда других не менее важных параметров.
Длина
Перед тем как рассчитать несущую способность и прогиб, нужно узнать длину каждой деревянной доски. Данный параметр определяется длиной пролёта. Тем не менее это не всё. Вы должны провести расчёт с некоторым запасом.
Важно! Если деревянные балки заделываться в стены — это напрямую влияет на их длину и все дальнейшие расчёты.
При подсчёте особое значение имеет материал, из которого сделан дом. Если это кирпич, доски будут монтироваться внутрь гнёзд. Приблизительная глубина около 100—150 мм.
Приблизительная глубина около 100—150 мм.
Когда речь идёт о деревянных постройках параметры согласно СНиПам сильно меняются. Теперь достаточно глубины в 70—90 мм. Естественно, что из-за этого также изменится конечная несущая способность.
Если в процессе монтажа применяются хомуты или кронштейны, то длина брёвен или досок соответствует проёму. Проще говоря, высчитайте расстояние от стены до стены и в итоге сможете узнать несущую способность всей конструкции.
Важно! При формировании ската крыши брёвна выносятся за стены на 30—50 сантиметров. Это нужно учесть при подсчёте способности конструкции противостоять нагрузкам.
К сожалению, далеко не всё зависит от фантазии архитектора, когда дело касается исключительно математики. Для обрезной доски максимальная длина шесть метров. В противном случае несущая способность уменьшается, а прогиб становится больше.
Само собой, что сейчас не редкость дома, у которых пролёт достигает 10—12 метров. В таком случае используется клееный брус. Он может быть двутавровым или же прямоугольным. Также для большей надёжности можно использовать опоры. В их качестве идеально подходят дополнительные стены или колоны.
В таком случае используется клееный брус. Он может быть двутавровым или же прямоугольным. Также для большей надёжности можно использовать опоры. В их качестве идеально подходят дополнительные стены или колоны.
Совет! Многие строители при необходимости перекрыть длинный пролёт используют фермы.
Общая информация по методологии расчёта
В большинстве случаев в малоэтажном строительстве применяются однопролётные балки. Они могут быть в виде брёвен, досок или брусьев. Длина элементов может варьироваться в большом диапазоне. В большинстве случаев она напрямую зависит от параметров строения, которые вы собираетесь возвести.
Внимание! Представленный в конце странички калькулятор расчета балок на прогиб позволит вам просчитать все значения с минимальными затратами времени. Чтобы воспользоваться программой, достаточно ввести базовые данные.
Роль несущих элементов в конструкции выполняют деревянные бруски, высота сечения которых составляет от 140 до 250 мм, толщина лежит в диапазоне 55—155 мм.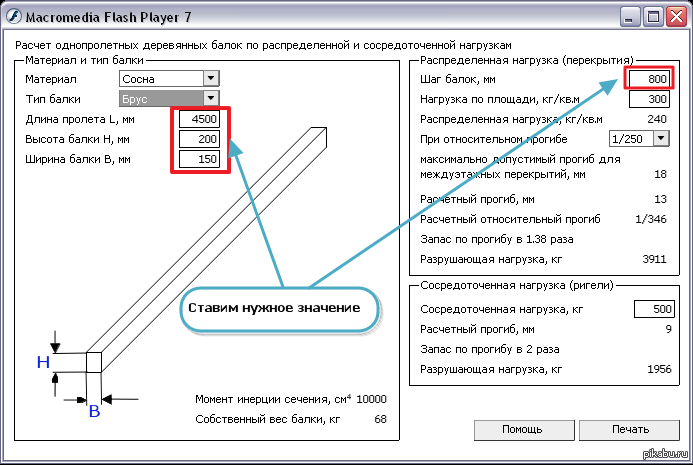 Это наиболее часто используемые параметры при расчёте несущей способности деревянных балок.
Это наиболее часто используемые параметры при расчёте несущей способности деревянных балок.
Очень часто профессиональные строители для того чтобы усилить конструкцию используют перекрёстную схему монтажа балок. Именно эта методика даёт наилучший результат при минимальных затратах времени и материалов.
Если рассматривать длину оптимального пролёта при расчёте несущей способности деревянных балок, то лучше всего ограничить фантазию архитектора в диапазоне от двух с половиной до четырёх метров.
Внимание! Лучшим сечением для деревянных балок считается площадь, у которой высота и ширина соотносятся как 1,5 к 1.
Как рассчитать несущую способность и прогиб
Стоит признать, что за множество лет практики в строительном ремесле был выработан некий канон, который чаще всего используют для того, чтобы провести расчёт несущей способности:
M/W<=Rд
Расшифруем значение каждой переменной в формуле:
- Буква М вначале формулы указывает на изгибающий момент.
 Он исчисляется в кгс*м.
Он исчисляется в кгс*м. - W обозначает момент сопротивления. Единицы измерения см3.
Расчёт прогиба деревянной балки является частью, представленной выше формулы. Буква М указывает нам на данный показатель. Чтобы узнать параметр применяется следующая формула:
M=(ql2)/8
В формуле расчёта прогиба есть всего две переменных, но именно они в наибольшей степени определяют, какой в конечном итоге будет несущая способность деревянной балки:
- Символ q показывает нагрузку, которую способна выдержать доска.
- В свою очередь буква l — это длина одной деревянной балки.
Внимание! Результат расчёт несущей способности и прогиба зависит от материала из которого сделана балка, а также от способа его обработки.
Насколько важно правильно рассчитать прогиб
Этот параметр крайне важен для прочности всей конструкции. Дело в том, что одной стойкости бруса недостаточно для долгой и надёжной службы, ведь со временем его прогиб под нагрузкой может увеличиваться.
Прогиб не просто портит эстетичный вид перекрытия. Если данный параметр превысит показатель в 1/250 от общей длины элемента перекрытия, то вероятность возникновения аварийной ситуации возрастёт в десятки раз.
Так зачем нужен калькулятор
Представленный ниже калькулятор позволит вам моментально просчитать прогиб, несущую способность и многие другие параметры без использования формул и подсчётов. Всего несколько секунд и данные по вашему будущему дому будут готовы.
Расчет деревянной балки перекрытия на прогиб, пример, таблица
Применяется и такое конструктивное решение, когда несущие элементы перекрытия являются частью стропильных конструкций. В этом случае балка является конструкцией для формирования свеса, то она опирается на мауэрлат и имеет выпуск за внешнюю грань каждой стены примерно на 500 мм. Это конструктивное решение может увеличить её длину примерно на 1 метр.
Производя подбор и расчет деревянных балок необходимо помнить, что самым оптимальным расстоянием, которое можно перекрывать, применяя эти конструктивные элементы, является 6 метровый пролет.
При необходимости перекрывать большие расстояния рекомендуется использование деревянных конструкций прямоугольного или двутаврового сечения изготовленных из клееного бруса или применять промежуточные конструкции, такие как стойки, колонны, декоративные арки и т.п.
Сбор нагрузок воздействующих на балки
Диапазон различного вида нагрузок действующих на несущие конструкции достаточно велик. Он различается исходя из целевого применения балки, то есть ответа на вопрос эта балка располагается в междуэтажном или чердачном перекрытии. Конструкции междуэтажных перекрытий несут нагрузку в основном только от веса самого перекрытия, от процесса жизнедеятельности людей которые там находятся и того производственного процесса который там проходит.
Так расчетная нагрузка на междуэтажное перекрытие в жилых зданиях равна 150кг/м2 х 1,3 = 195 кг/м2.
Коэффициент 1,3 обеспечивает надежность работы конструкции. Вес междуэтажного перекрытия включает вес балок, полов, конструкций потолка, утеплителя. При производстве расчетов вес междуэтажного перекрытия лучше всего рассчитывать в каждом случае индивидуально.
При производстве расчетов вес междуэтажного перекрытия лучше всего рассчитывать в каждом случае индивидуально.
Нагрузка на чердачное перекрытие, эксплуатация которого не предусматривает 70 кг/м2 х 1,3 = 91 кг/м².
Вес самого чердачного перекрытия включает в себя вес балок, утеплителя, материала зашивки и составляет 50 кг/м2. В случае, если балка является не только чердачным перекрытием, но и входит в конструкцию стропильной системы здания, то её расчет производится в составе стропильных конструкций.
В случае, когда величина прогиба превышает указанные величины, это может нанести существенные деформационные изменения в геометрии потолочных конструкций. Так при длине балки перекрытия 6 метров величина допустимого прогиба будет составлять 17 мм. Если предположить, что потолок в помещении будет из гипсокартонных плит, то образование трещин неминуемо. Поэтому производя расчет, следует сразу же учитывать материал, из которого будет выполняться конструкция потолка.
Расчет деревянной балки перекрытия
Предлагаем вашему вниманию онлайн калькулятор расчета деревянных балок перекрытия. Этот удобный и эффективный строительный калькулятор поможет вам легко и точно произвести один из самых трудных конструкционных расчетов.
Деревянные балки межэтажного перекрытия являются несущей конструкцией. Они воспринимают нагрузку, ложащуюся на межэтажное перекрытие, и, таким образом, от их надежности в значительной степени зависит сохранность здания и безопасность его обитателей. Расчет деревянной балки перекрытия необходим для того, чтобы определить, выдержит ли балка с определенными характеристиками предполагаемую вертикальную нагрузку или же вычислить, какую именно вертикальную нагрузку способна выдержать деревянная балка с заданными характеристиками.
Еще один важный вид строительных расчетов, касающийся балок перекрытия – расчет прогиба деревянной балки. Даже если балка достаточно прочна, чтобы не переломиться, под постоянной нагрузкой она может постепенно прогнуться. А это портит вид потолка и создает различные неудобства. Да и жить под прогнувшимися балками, даже будучи уверенным в их прочности, не слишком приятно. Согласно стандартным нормам прогиб не должен быть более 1/250 длины деревянной балки. Калькулятор расчета деревянных балок поможет вам точно подсчитать величину расчетного прогиба балки при заданных габаритах и типе древесины.
Калькулятор расчета деревянных балок поможет вам точно подсчитать величину расчетного прогиба балки при заданных габаритах и типе древесины.
Программа расчета деревянных балок
Программа расчета деревянных балок перекрытия — небольшой и удобный инструмент, который упростит основные расчеты по определению сечения бруса и шага его установки при устройстве межэтажных перекрытий.
Инструкция по работе с программой
Рассмотренная программа небольшая и дополнительной установки не требует.
Интерфейс программыЧтобы было понятнее, рассмотрим каждый пункт программы:
- Материал — выбираем требуемый материал бруса или бревна.
- Тип балки — брус или бревно.

- Размеры — длина, высота, ширина.
- Шаг балок — расстояние между балками. Изменяя данный параметр (как и размеры) можно добиться оптимального соотношения.
- Нагрузка по площади. Как правило, расчет нагрузки на перекрытия производится на этапе проектирования специалистами, но выполнить его можно и самостоятельно. Прежде всего, учитывается вес материалов, из которых изготовлено перекрытие. Например, чердачное перекрытие, утепленное легким материалом (например, минеральной ватой), с легкой подшивкой выдерживает нагрузку от собственного веса в пределах 50 кг/м². Эксплуатационная нагрузка определяется в соответствии с нормативными документами. Для чердачного перекрытия из деревянных основных материалов и с легкими утеплителем и подшивкой эксплуатационная нагрузка в соответствии со СНиП 2.01.07-85 вычисляется таким путем: 70*1,3=90 кг/м². 70 кг/м². В этом расчете берется нагрузка в соответствии с нормативами, а 1,3 – коэффициент запаса.
 Общая нагрузка вычисляется путем сложения: 50+90=140 кг/м². Для надежности цифру рекомендуется округлить немного в большую сторону. В данном случае можно принимать общую нагрузку за 150 кг/м². Если чердачное помещение планируется интенсивно эксплуатировать, то требуется увеличить в расчете нормативное значение нагрузки до 150. В этом случае расчет будет выглядеть следующим образом: 50+150*1,3=245 кг/м². После округления в большую сторону – 250 кг/м². Также следует проводить расчет таким образом, в случае если используются более тяжелые материалы: утеплители, подшивка для заполнения межбалочного пространства. Если на чердаке будет обустраиваться мансарда, то необходимо принимать во внимание вес пола и мебели. В этом случае общая нагрузка может составить до 400 кг/м².
Общая нагрузка вычисляется путем сложения: 50+90=140 кг/м². Для надежности цифру рекомендуется округлить немного в большую сторону. В данном случае можно принимать общую нагрузку за 150 кг/м². Если чердачное помещение планируется интенсивно эксплуатировать, то требуется увеличить в расчете нормативное значение нагрузки до 150. В этом случае расчет будет выглядеть следующим образом: 50+150*1,3=245 кг/м². После округления в большую сторону – 250 кг/м². Также следует проводить расчет таким образом, в случае если используются более тяжелые материалы: утеплители, подшивка для заполнения межбалочного пространства. Если на чердаке будет обустраиваться мансарда, то необходимо принимать во внимание вес пола и мебели. В этом случае общая нагрузка может составить до 400 кг/м². - При относительном прогибе. Разрушение деревянной балки обычно происходит от поперечного изгиба, при котором в сечении балки возникают сжимающие и растягивающие напряжения. Вначале древесина работает упруго, затем возникают пластические деформации, при этом в сжатой зоне происходит смятие крайних волокон (складки), нейтральная ось опускается ниже центра тяжести.
 При дальнейшем росте изгибающего момента пластические деформации растут и происходит разрушение в результате разрыва крайних растянутых волокон. Максимальный относительный прогиб балок и прогонов покрытий не должен превышать 1/200.
При дальнейшем росте изгибающего момента пластические деформации растут и происходит разрушение в результате разрыва крайних растянутых волокон. Максимальный относительный прогиб балок и прогонов покрытий не должен превышать 1/200. - Среднеточечная нагрузка (для ригелей) — это нагрузка, взятая с плиты (полная) плюс собственный вес ригеля.
Похожие записи по метке:
Бесплатный калькулятор луча | ClearCalcs
Как использовать бесплатный калькулятор балки
Калькулятор балки ClearCalcs позволяет пользователю ввести геометрию и загрузку балки для анализа за несколько простых шагов. Затем он определяет изгибающий момент, диаграммы сдвига и прогиба, а также максимальные требования, используя мощный механизм анализа методом конечных элементов.
Регистрация учетной записи ClearCalcs откроет дополнительные расширенные функции для проектирования и анализа балок и множества других структурных элементов.ClearCalcs позволяет проектировать из стали, бетона и дерева в соответствии со стандартами Австралии, США и ЕС.
Лист разделен на три основных раздела:
- «Ключевые свойства», где пользователь вводит геометрию выбранного сечения и опор балки.
- «Нагрузки», где можно ввести распределенные, точечные и приложенные моментные нагрузки,
- «Сводка», в котором отображаются основные выходные данные и диаграммы.
Раздел «Комментарии» также включен для того, чтобы пользователь мог оставить какие-либо конкретные примечания по дизайну.Щелчок по любой из меток ввода / свойства дает описательное справочное объяснение.
1. Свойства входных клавиш
Свойства балки и сечения задаются путем ввода непосредственно в поля ввода.
Длина балки — это общая длина балки, включая все пролеты балки, в мм или футах.
Модуль Юнга установлен на значение по умолчанию 200000 МПа или 29000 тысяч фунтов на квадратный дюйм для конструкционной стали, но его можно изменить. Пользователь.
Площадь поперечного сечения зависит от выбранного сечения балки и по умолчанию соответствует значениям для обычной стальной балки.
Второй момент площади (или момент инерции) также зависит от выбранного сечения балки и снова по умолчанию соответствует свойствам обычной стальной балки.
Свойства E, A и Ix для других секций балки можно получить из библиотеки свойств секций ClearCalcs. Кроме того, вы можете создать свой собственный раздел, используя наш бесплатный калькулятор момента инерции.
Положение опор слева позволяет пользователю вводить любое количество опор и указывать их положение по длине балки.Тип опоры может быть закрепленным (фиксированный в перемещении, свободном вращении) или фиксированным (фиксированный как при перемещении, так и при повороте) и выбирается из раскрывающегося меню. Требуется минимум одна фиксированная опора или две штифтовые опоры.
Требуется минимум одна фиксированная опора или две штифтовые опоры.
Вычислитель балки также позволяет использовать пролет консолей на каждом конце, поскольку положение первой опоры не обязательно должно быть равно 0 мм, а положение последней опоры не обязательно должно быть равно длине балки.
Реакции на каждой из опор автоматически обновляются по мере добавления, изменения или удаления опор в зависимости от указанной нагрузки.
2. Входные нагрузки
Калькулятор поддерживает различные типы нагрузок, которые можно применять в комбинации. Каждой загрузке может быть присвоено имя пользователем.
Знаковое обозначение, используемое для нагружения (показаны положительные значения):
Распределенные нагрузки указываются в единицах силы на единицу длины, кН / м или plf, вдоль балки и могут применяться между любыми двумя точками. В калькуляторе можно использовать два разных типа:
Равномерная нагрузка имеет постоянную величину по всей длине приложения. Следовательно, начальная и конечная величины, указанные пользователем, должны быть одинаковыми.
Следовательно, начальная и конечная величины, указанные пользователем, должны быть одинаковыми.
Линейные нагрузки имеют переменную величину по длине приложения. Различные начальные и конечные величины должны быть указаны пользователем, и они могут использоваться для представления треугольных или трапециевидных нагрузок.
Точечные нагрузки указываются в единицах силы, кН или тысячах фунтов, и площади, приложенной в дискретных точках вдоль балки. Например, они могут представлять реакции других элементов, соединенных с балкой.Пользователь вводит имя, величину и местоположение слева от луча.
На приведенной ниже диаграмме из сводного раздела показана двухпролетная неразрезная балка с линейно распределенной нагрузкой участка и точечной нагрузкой.
3. Итоговые результаты вычислений
После задания нагрузки и геометрии калькулятор автоматически использует механизм конечно-элементного анализа ClearCalcs для определения моментов, поперечных сил и прогибов. Максимальные значения каждого из них выводятся как «Требование момента» , «Требование сдвига», и «Прогиб» вместе с диаграммами по длине балки.
Максимальные значения каждого из них выводятся как «Требование момента» , «Требование сдвига», и «Прогиб» вместе с диаграммами по длине балки.
Положительные значения означают отклонение вниз, а отрицательные значения — отклонение вверх. Знаковое соглашение, используемое на диаграммах поперечной силы и изгибающего момента, следующее (показаны положительные значения):
Использование курсора для наведения курсора на любую точку на диаграммах изгибающего момента, поперечной силы или прогиба дает конкретные значения в этом месте вдоль балки. В приведенном ниже примере показаны выходные параметры для двухпролетной неразрезной балки с линейно распределенной коммутационной нагрузкой и точечной нагрузкой.
Калькулятор отклонения балки
Этот калькулятор отклонения балки поможет вам определить максимальное отклонение балки для балок с простой опорой и консольных балок, несущих простых конфигураций нагрузки .Вы можете выбрать один из нескольких типов нагрузки, которые могут воздействовать на балку любой длины по вашему желанию. Величина и расположение этих нагрузок влияют на то, насколько балка изгибается. В этом калькуляторе отклонения балки вы узнаете о различных формулах отклонения балки , используемых для расчета прогибов балок без опоры и прогибов консольных балок. Вы также узнаете, как модуль упругости балки и момент инерции ее поперечного сечения влияют на расчетный максимальный прогиб балки.
Величина и расположение этих нагрузок влияют на то, насколько балка изгибается. В этом калькуляторе отклонения балки вы узнаете о различных формулах отклонения балки , используемых для расчета прогибов балок без опоры и прогибов консольных балок. Вы также узнаете, как модуль упругости балки и момент инерции ее поперечного сечения влияют на расчетный максимальный прогиб балки.
Что такое прогиб балки и изгиб балки
В строительстве мы обычно используем каркасных конструкций , которые удерживаются фундаментом в земле. Эти каркасные конструкции подобны каркасам зданий, домов и даже мостов. В раме мы называем вертикальное обрамление колонн , а горизонтальные балки . Балки — это длинные элементы конструкции, которые несут нагрузки, создаваемые горизонтальными плитами конструкций, включая перекрытия и крыши.
Когда балки несут слишком тяжелые для них нагрузки, они начинают гнуться.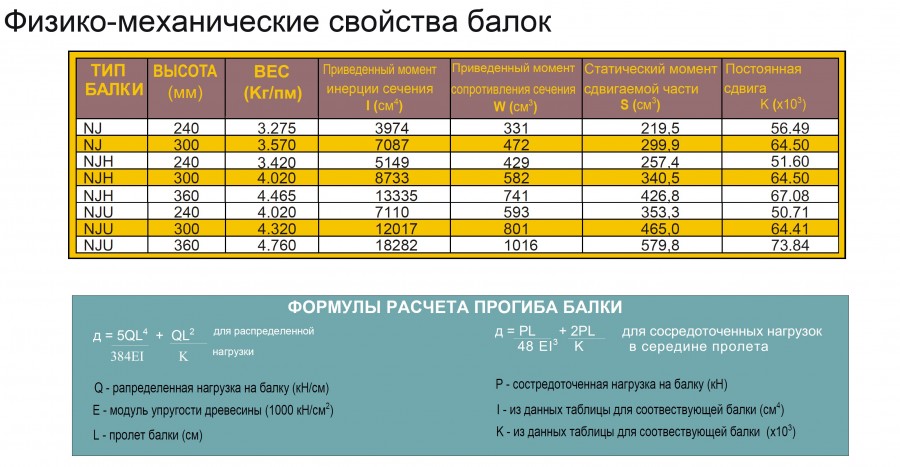 Мы называем величину изгиба балки прогибом балки . Отклонение балки — это вертикальное смещение точки вдоль центра тяжести балки. Мы также можем рассматривать поверхность балки как опорную точку, если нет изменений в высоте или глубине балки во время изгиба.
Мы называем величину изгиба балки прогибом балки . Отклонение балки — это вертикальное смещение точки вдоль центра тяжести балки. Мы также можем рассматривать поверхность балки как опорную точку, если нет изменений в высоте или глубине балки во время изгиба.
Как рассчитать максимальный прогиб балки
Мы снабдили наш калькулятор отклонения балки формулами, которые инженеры и студенты-инженеры используют для быстрого определения максимального отклонения, которое будет испытывать конкретная балка из-за нагрузки, которую она несет.Однако эти формулы могут решать только простые нагрузки и их комбинацию. Мы составили для вас таблицы этих формул, как показано ниже:
Формулы прогиба балок с простой опорой
Формулы прогиба консольной балки
Метод наложения
Для расчета максимального прогиба балки с комбинацией нагрузок мы можем использовать метод наложения . Метод наложения утверждает, что мы можем приблизительно оценить полное отклонение балки, сложив вместе все отклонения, вызванные каждой конфигурацией нагрузки. Однако этот метод дает нам лишь приблизительное значение фактического максимального прогиба. Расчет сложных нагрузок потребует от нас использования так называемого метода двойного интегрирования .
Однако этот метод дает нам лишь приблизительное значение фактического максимального прогиба. Расчет сложных нагрузок потребует от нас использования так называемого метода двойного интегрирования .
Жесткость балки
Расчет отклонения балки требует знания жесткости балки и величины силы или нагрузки, которые могут повлиять на изгиб балки. Мы можем определить жесткость балки, умножив модуль упругости балки E на ее момент инерции I .Модуль упругости зависит от материала балки. Чем выше модуль упругости материала, тем больше прогиб может выдержать огромные нагрузки, прежде чем достигнет предела разрушения. Модуль упругости бетона составляет 15-50 ГПа (гигапаскалей), а у стали — около 200 ГПа и выше. Эта разница в значениях модуля упругости показывает, что бетон может выдерживать лишь небольшой прогиб и трескается быстрее, чем сталь.
Вы можете узнать больше о модуле упругости, воспользовавшись нашим калькулятором напряжений. С другой стороны, чтобы определить момент инерции для определенного поперечного сечения балки, вы можете воспользоваться нашим калькулятором момента инерции. Момент инерции представляет собой величину сопротивления материала вращательному движению. Момент инерции зависит от размеров поперечного сечения материала.
С другой стороны, чтобы определить момент инерции для определенного поперечного сечения балки, вы можете воспользоваться нашим калькулятором момента инерции. Момент инерции представляет собой величину сопротивления материала вращательному движению. Момент инерции зависит от размеров поперечного сечения материала.
Момент инерции также зависит от оси вращения материала. Чтобы лучше понять эту концепцию, давайте рассмотрим поперечное сечение прямоугольной балки шириной 20 см и высотой 30 см.Используя формулы, которые вы также можете увидеть в нашем калькуляторе момента инерции, мы можем вычислить значения момента инерции этого поперечного сечения следующим образом:
Iₓ = ширина * высота³ / 12
= 20 * (30³) / 12
= 45000 см⁴
Iᵧ = высота * ширина³ / 12
= 30 * (20³) / 12
= 20,000 см⁴
Обратите внимание на два значения момента инерции. Это потому, что мы можем рассматривать изгиб балки по вертикали (по оси x, то есть Iₓ) или по горизонтали (по оси y, то есть Iᵧ). Поскольку мы учитываем отклонение балки при вертикальном изгибе, для наших расчетов всегда нужно использовать Iₓ . Полученные нами значения говорят нам о том, что балку труднее изгибать при вертикальной нагрузке и легче изгибать, если она подвергается горизонтальной нагрузке. Эта разница в значениях момента инерции является причиной того, что мы видим балки в этой конфигурации, в которой ее высота больше, чем ее ширина.
Поскольку мы учитываем отклонение балки при вертикальном изгибе, для наших расчетов всегда нужно использовать Iₓ . Полученные нами значения говорят нам о том, что балку труднее изгибать при вертикальной нагрузке и легче изгибать, если она подвергается горизонтальной нагрузке. Эта разница в значениях момента инерции является причиной того, что мы видим балки в этой конфигурации, в которой ее высота больше, чем ее ширина.
Понимание формул прогиба балки
Теперь, когда мы знаем концепции модуля упругости и момента инерции, мы можем теперь понять, почему эти переменные являются знаменателями в наших формулах отклонения балки.Формулы показывают, что чем жестче балка, тем меньше будет ее прогиб. Однако, изучив наши формулы, мы также можем сказать, что длина балки также напрямую влияет на прогиб балки. Чем длиннее балка, тем больше она может изгибаться и тем больше может быть прогиб.
С другой стороны, нагрузки влияют на отклонение балки двумя способами: направление отклонения и величина отклонения . Нисходящие нагрузки склонны отклонять балку вниз.Нагрузки могут быть в виде точечной нагрузки, линейного давления или моментной нагрузки. Формулы в этом калькуляторе ориентированы только на нисходящие или восходящие направления для точечной нагрузки и распределенных нагрузок. Распределенные нагрузки аналогичны давлению, но учитывают только длину балки, а не ширину балки. Формулы в этом калькуляторе также учитывают момент или крутящий момент нагрузки как по часовой стрелке, так и против часовой стрелки. Просто проконсультируйтесь по направлениям стрелок на соответствующем изображении формулы, чтобы выяснить, в каком направлении имеется положительное значение нагрузки.
Нисходящие нагрузки склонны отклонять балку вниз.Нагрузки могут быть в виде точечной нагрузки, линейного давления или моментной нагрузки. Формулы в этом калькуляторе ориентированы только на нисходящие или восходящие направления для точечной нагрузки и распределенных нагрузок. Распределенные нагрузки аналогичны давлению, но учитывают только длину балки, а не ширину балки. Формулы в этом калькуляторе также учитывают момент или крутящий момент нагрузки как по часовой стрелке, так и против часовой стрелки. Просто проконсультируйтесь по направлениям стрелок на соответствующем изображении формулы, чтобы выяснить, в каком направлении имеется положительное значение нагрузки.
Пример расчета прогиба балки
Для примера расчета прогиба балки рассмотрим простую деревянную скамью с ножками на расстоянии 1,5 метра друг от друга в их центрах. Допустим, у нас есть доска из восточной белой сосны толщиной 4 см и шириной 30 см, которая служит сиденьем для этой скамейки. Мы можем рассматривать это сиденье как балку, которая отклоняется, когда кто-то садится на скамейку. Зная размеры этого сиденья, мы можем вычислить его момент инерции, как в нашем примере выше.Поскольку нам нужно рассчитать Iₓ, его момент инерции будет:
Зная размеры этого сиденья, мы можем вычислить его момент инерции, как в нашем примере выше.Поскольку нам нужно рассчитать Iₓ, его момент инерции будет:
Iₓ = ширина * высота³ / 12
= 30 * (4³) / 12
= 160,0 см⁴ или 1,6x10⁻⁶ м⁴
Сосна белая восточная имеет модуль упругости 6,800 МПа (6,8x10⁹ Па) , что является значением, которое мы получили из Справочника по древесине. Вы также можете легко получить значение модуля упругости для других материалов, таких как сталь и бетон, в Интернете или в местной библиотеке.Теперь, когда мы знаем эти значения, давайте рассмотрим нагрузку, которую будет нести этот стенд. Предположим, что ребенок 400 N сидит в центре скамейки. Теперь мы можем рассчитать прогиб сиденья скамейки из-за точечной нагрузки в его центре:
δₘₐₓ = P * L³ / (48 * E * I)
δₘₐₓ = (400 Н) * (1,5 м) ³ / (48 * 6,8x10⁹ Па * 1,6x10⁻⁶ м⁴)
δₘₐₓ = 0,002585 m = 2,5850 мм
Это означает, что многоместное сиденье прогнется примерно на 2. 6 миллиметров на от исходного положения, когда ребенок сидит посередине скамейки.
6 миллиметров на от исходного положения, когда ребенок сидит посередине скамейки.
Если вы нашли эту тему интересной и хотели бы узнать больше о прочности материалов, вам также может понравиться наш калькулятор запаса прочности. Вы также можете воспользоваться нашим конвертером силы, если хотите изучить различные единицы измерения точечных нагрузок и расчета сил.
Бесплатный калькулятор луча | Калькулятор изгибающего момента, поперечной силы и прогиба
Добро пожаловать в наш бесплатный онлайн-калькулятор диаграмм изгибающего момента и поперечной силы, который может генерировать диаграммы реакций, поперечных сил (SFD) и изгибающих моментов (BMD) консольной балки или просто поддерживаемой балки.Используйте этот калькулятор пролета балки, чтобы определить реакции на опоры, построить диаграмму сдвига и момента для балки и рассчитать прогиб стальной или деревянной балки. Бесплатный онлайн-калькулятор балки для создания реакций, расчета прогиба стальной или деревянной балки, построения диаграмм сдвига и момента балки.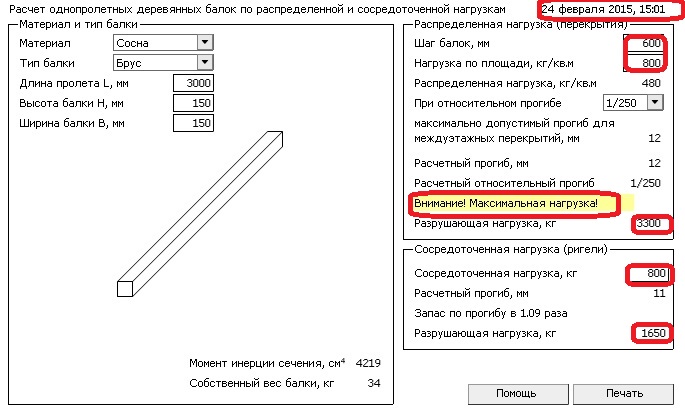 Это бесплатная версия нашего полного программного обеспечения SkyCiv Beam. Доступ к нему можно получить из любой из наших Платных учетных записей, которая также включает в себя полное программное обеспечение для структурного анализа.
Это бесплатная версия нашего полного программного обеспечения SkyCiv Beam. Доступ к нему можно получить из любой из наших Платных учетных записей, которая также включает в себя полное программное обеспечение для структурного анализа.
Используйте интерактивное окно выше, чтобы просмотреть и удалить длину балки, опоры и добавленные нагрузки. Любые внесенные изменения автоматически перерисовывают диаграмму свободного тела для любой балки с опорой или консолью. Калькулятор реакции балки и расчет изгибающего момента запускаются после нажатия кнопки «Решить» и автоматически генерируют диаграммы сдвига и изгибающего момента. Вы также можете щелкнуть отдельные элементы этого калькулятора балки LVL, чтобы редактировать модель.
Калькулятор пролета балки легко рассчитает реакции на опорах.Он может рассчитывать реакции на опорах консольных или простых балок. Это включает в себя расчет реакций для консольной балки, которая имеет реакцию изгибающего момента, а также силы реакции x, y.
Вышеупомянутый калькулятор пролета стальной балки — это универсальный инструмент для проектирования конструкций, используемый для расчета изгибающего момента в алюминиевой, деревянной или стальной балке. Его также можно использовать в качестве калькулятора несущей способности балки, используя его в качестве калькулятора напряжения изгиба или напряжения сдвига. Он способен выдерживать до 2 различных сосредоточенных точечных нагрузок, 2 распределенных нагрузки и 2 момента.Распределенные нагрузки могут быть расположены так, чтобы они были равномерно распределенными нагрузками (UDL), треугольными распределенными нагрузками или трапециевидными распределенными нагрузками. Все нагрузки и моменты могут иметь направление как вверх, так и вниз по величине, что должно учитывать наиболее распространенные ситуации анализа балок. Расчет изгибающего момента и поперечной силы может занять до 10 секунд, и обратите внимание, что вы будете перенаправлены на новую страницу с реакциями, диаграммой поперечной силы и диаграммой изгибающего момента балки.
Одна из самых мощных функций — использование его в качестве калькулятора отклонения балки (или калькулятора смещения балки). Это можно использовать для наблюдения расчетного прогиба балки с опорой или консольной балки. Возможность добавлять формы сечения и материалы делает его полезным в качестве калькулятора деревянных балок или в качестве калькулятора стальных балок для проектирования балок lvl или i. На данный момент эта функция доступна в SkyCiv Beam, который имеет гораздо больше функций для проектирования деревянных, бетонных и стальных балок.
SkyCiv предлагает инженерам широкий спектр программного обеспечения для структурного анализа и проектирования облачных вычислений. Как постоянно развивающаяся технологическая компания, мы стремимся внедрять инновации и совершенствовать существующие рабочие процессы, чтобы сэкономить время инженеров в их рабочих процессах и проектах.
Балки — поддерживаются с обеих сторон
Напряжение в изгибаемой балке можно выразить как
σ = y M / I (1)
, где
σ = напряжение (Па (Н / м ) 2 ), Н / мм 2 , psi)
y = расстояние до точки от нейтральной оси (м, мм, дюйм)
M = изгибающий момент (Нм, фунт дюйм)
I = момент инерции (м 4 , мм 4 , в 4 )
Калькулятор ниже можно использовать для расчета максимального напряжения и прогиба балок с одной одиночной или равномерно распределенной нагрузкой.
Балка, поддерживаемая на обоих концах — равномерная непрерывная распределенная нагрузка
Момент в балке с равномерной нагрузкой, поддерживаемой на обоих концах в положении x, может быть выражен как
M x = qx (L — x) / 2 (2)
где
M x = момент в положении x (Нм, фунт дюйм)
x = расстояние от конца (м, мм, дюйм)
Максимум момент находится в центре балки на расстоянии L / 2 и может быть выражен как
M max = q L 2 /8 (2a)
где
M макс = максимальный момент ( Нм, фунт-дюйм)
q = равномерная нагрузка на единицу длины балки (Н / м, Н / мм, фунт / дюйм)
9024 0 L = длина балки (м, мм, дюйм)
Максимальное напряжение
Уравнения 1 и 2a могут быть объединены для выражения максимального напряжения в балке с равномерной поддерживаемой нагрузкой на обоих концах на расстоянии L / 2 как
σ max = y max q L 2 / (8 I) (2b)
где
σ max = максимальное напряжение (Па (Н / м 2 ), Н / мм 2 , psi)
y max = расстояние до крайней точки от нейтральной оси (м, мм, дюйм)
- 1 Н / м 2 = 1×10 -6 Н / мм 2 = 1 Па = 1.4504×10 -4 фунтов на кв. Дюйм
- 1 фунт / дюйм (фунт / дюйм 2 ) = 144 фунта на квадратный дюйм (фунт на / фут 2 ) = 6 894,8 Па (Н / м 2 ) = 6,895×10 — 3 Н / мм 2
Максимальный прогиб :
δ max = 5 q L 4 / (384 EI) (2c)
где 07
83 903 макс
= максимальный прогиб (м, мм, дюйм)E = Модуль упругости (Па (Н / м 2 ), Н / мм 2 , psi)
Прогиб в положении x:
δ x = qx ( L 3 — 2 L x 2 + x 3 ) / (24 EI) (2d)
Примечание! — прогиб часто является ограничивающим фактором при проектировании балки.Для некоторых применений балки должны быть прочнее, чем требуется при максимальных нагрузках, чтобы избежать недопустимого прогиба.
Силы, действующие на концы:
R 1 = R 2
= q L / 2 (2e)
где
R = сила реакции (Н, фунт)
Пример — балка с равномерной нагрузкой, метрические единицы
Балка UB 305 x 127 x 42 длиной 5000 мм несет равномерную нагрузку 6 Н / мм .Момент инерции балки составляет 8196 см 4 (81960000 мм 4 ) , а модуль упругости стали, используемой в балке, составляет 200 ГПа (200000 Н / мм 2 ) . Высота балки 300 мм (расстояние от крайней точки до нейтральной оси 150 мм ).
Максимальное напряжение в балке можно рассчитать
σ max = (150 мм) (6 Н / мм) (5000 мм) 2 / (8 (81960000 мм 4 ))
= 34.3 Н / мм 2
= 34,3 10 6 Н / м 2 (Па)
= 34,3 МПа
Максимальный прогиб балки можно рассчитать 07
07
δ макс = 5 (6 Н / мм) (5000 мм) 4 / (( 200000 Н / мм 2 ) ( 81960000 мм 4 ) 384)
= 2,98 мм
Калькулятор балки с равномерной нагрузкой — метрические единицы
- 1 мм 4 = 10 -4 см 4 = 10 -12 м 4 900 1 см 4 = 10 -8 м = 10 4 мм
- 1 дюйм 4 = 4.16×10 5 мм 4 = 41,6 см 4
- 1 Н / мм 2 = 10 6 Н / м 2 (Па)
Расчет балки равномерной нагрузки — Британские единицы
Пример — балка с равномерной нагрузкой, британские единицы
Максимальное напряжение в стальной широкополочной балке W 12 x 35 дюймов, 100 дюймов длиной , момент инерции 285 дюймов 4 , модуль упругости 200 psi
, при равномерной нагрузке 100 фунтов / дюйм можно рассчитать как
σ max = y max q L 2 / (8 I)
= (6.25 дюймов (100 фунтов / дюйм) (100 дюймов) 2 / (8 (285 дюймов 4 ))
= 2741 (фунт / дюйм 2 , psi)
Максимальное отклонение может рассчитывается как
δ max = 5 q L 4 / (EI 384)
= 5 (100 фунтов / дюйм) (100 дюймов) 4 / ((2
00 фунтов / дюйм
2 ) (285 дюймов 4 ) 384)= 0,016 дюйма
Балка, поддерживаемая на обоих концах — нагрузка в центре
Максимальный момент в балке с центральной нагрузкой, поддерживаемой с обоих концов :
M max = FL / 4 (3a)
Максимальное напряжение
Максимальное напряжение в балке с одноцентровой нагрузкой, поддерживаемой на обоих концах:
σ max = y max FL / (4 I) (3b) 903 31
, где
F = нагрузка (Н, фунт)
Максимальный прогиб можно выразить как
δ max = FL 3 / (48 EI) (3c)
Силы, действующие на концы:
R 1 = R 2
= F / 2 (3d)
Расчет балки с одним центром нагрузки — метрические единицы
Калькулятор балки с одним центром нагрузки — британская система мер Единицы измерения
Пример — балка с одинарной центральной нагрузкой
Максимальное напряжение в стальной широкополочной балке шириной 12 x 35 дюймов, 100 дюймов длиной , момент инерции 285 дюймов 4 , модуль упругости 200 psi
, с центральной нагрузкой 10000 фунтов можно рассчитать как
σ max = y max FL / (4 I)
= (6.25 дюймов) (10000 фунтов) (100 дюймов) / (4 (285 дюймов 4 ))
= 5482 (фунт / дюйм 2 , psi)
Максимальный прогиб можно рассчитать как
δ макс = FL 3 / EI 48
= (10000 фунтов / дюйм) (100 дюймов) 3 / ((200 фунтов / дюйм
2 ) (285 дюймов 4 ) 48 )
= 0,025 дюйма
Некоторые типичные пределы отклонения по вертикали
- Полное отклонение: пролет / 250
- Прогиб при динамической нагрузке: пролет / 360
- консоли: пролет / 180
- Балки деревянных перекрытий в домашних условиях: пролет / 330 (макс. 14 мм)
- хрупкие элементы: пролет / 500
- подкрановые балки: пролет / 600
Балка, поддерживаемая на обоих концах — эксцентричная нагрузка
Максимальный момент в балке с одиночной эксцентричной нагрузкой в точке нагрузки:
M макс = F ab / L (4a)
Максимальное напряжение
Максимальное напряжение в балке с одной центральной нагрузкой, поддерживаемой с обоих концов:
σ max = y max F ab / (LI) (4b)
Максимальный прогиб в точке нагрузки можно выразить как
δ F = F a 2 b 2 / (3 EIL) (4c)
Силы, действующие на концы:
R 1 = F b / L (4d)
R 2 = F a / L (4e)
Балка, поддерживаемая на обоих концах — две эксцентриковые нагрузки
Максимальный момент (между нагрузками) в балке с двумя эксцентрическими нагрузками:
M max = F a (5a)
Максимальное напряжение
Максимальное напряжение в балке с двумя эксцентрическими нагрузками, поддерживаемыми на обоих концах:
σ max = y max F a / I (5b)
Максимум прогиб в точке нагрузки можно выразить как
δ F = F a (3L 2 — 4 a 2 ) / (24 EI) (5c)
Силы, действующие на концы:
R 1 = R 2
= F (5d)
Вставьте балки в свою модель Sketchup с помощью Engineering ToolBox Sketchup Extension
Балка поддерживается на обоих концах —
нагрузки
Максимальный момент (между нагрузками) в балке с тремя точечными нагрузками:
M max 90 284 = FL / 2 (6a)
Максимальное напряжение
Максимальное напряжение в балке с тремя точечными нагрузками, поддерживаемыми с обоих концов:
σ max = y max FL / (2 I) ( 6b)
Максимальный прогиб в центре балки можно выразить как
δ F = FL 3 / (20.22 E I) (6c)
Силы, действующие на концы:
R 1 = R 2
= 1,5 F (6d)
Расчет балки
Калькулятор отклонения балки
Этот калькулятор основан на теории пучков Эйлера-Бернулли. Уравнение Эйлера-Бернулли описывает взаимосвязь между прогибом балки и приложенными внешними силами.2) `
Калькулятор момента пучка и поперечной силы
Мы используем эти уравнения вместе с граничными условиями и нагрузками для наших балок, чтобы получить замкнутую форму решения для конфигураций балок, показанных на этой странице (балки с простой опорой и консольные балки). В Калькулятор балок использует эти уравнения для расчета изгибающего момента, поперечной силы, наклона и прогиба. диаграммы.
Калькулятор балок — отличный инструмент для быстрой проверки сил в балках.Используйте это, чтобы помочь вам в дизайне сталь, дерево и бетонные балки при различных условиях нагружения. Также помните, что вы можете добавлять результаты из балок все вместе с использованием метод суперпозиция.
Калькулятор стальных, деревянных и бетонных балок
Конечно, не всегда возможно (или практично) получить решение в замкнутой форме для некоторой балки. конфигурации.Если у вас стальная, деревянная или бетонная балка со сложными граничными условиями и нагрузками вам лучше решить проблему численно с помощью одного из наших инструментов анализа методом конечных элементов. Если ты не беспокоясь о конструктивных кодах и сравнивая потребность в луче и его пропускную способность, попробуйте наши простые в использовании Калькулятор сдвига и момента. Если вам нужны полные проверки конструкции с помощью AISC 360, NDS, ASD и LRFD для конструкции стальных или деревянных балок и вы хотите создать свой следующий луч за считанные минуты, вам может понравиться наш Инструмент Beam Designer.
Конструкция балок из стали и дерева по стандарту AISC по стандарту NDS
Наша цель с WebStructural — вернуть инженерное сообщество, предоставляя бесплатные, облачное приложение для проектирования стальных и деревянных балок. Нечего устанавливать, просто перейдите на наш Бесплатный конструктор стальных и деревянных балок и приступайте к проектированию! Если вам нравится инструмент и решите, что хотите сохранить и распечатать проекты, которые можно обновить за 19 долларов. ежемесячно.Нет долгосрочного контракта. Отмените в любой момент, мы сохраним ваши проекты, и вы сможете повторно подписаться позже чтобы получить к ним доступ.Другие бесплатные онлайн-калькуляторы
Мы создаем элегантное и мощное программное обеспечение для проектирования конструкций и расчета конструкций. Попробуйте некоторые из наших другие бесплатные инструменты:
Расчет деревянной балки для прочности, пример
Деревянная балка AB пролетом 5 м, шириной 100 мм и высотой 200 мм должна выдерживать три сосредоточенные нагрузки, показанные на рисунке.Выбранный сорт древесины имеет следующие допустимые материалы; τ все = 1 МПа и σ все = 10 МПа.
Рассчитать максимальное напряжение сдвига и нормальные напряжения для выбранной древесины. балка для данных условий нагружения.
Решение:
Шаг 1: Запишите входные параметры (включая свойства материала), которые определено в образце примера.
| ОБЗОР ВХОДНЫХ СВОЙСТВ | ||
| Параметр | Значение | |
| Ширина бруса [b] | 200 | мм |
| Высота бруса [H] | 100 | мм |
| Допустимое напряжение сдвига [τ все ] | 1 | МПа |
| Допустимое нормальное напряжение [σ все ] | 10 | МПа |
| Тип балки | Балка с простой опорой с множественными точечными нагрузками | |
Шаг 2. Посетите страницу «Пример расчета просто поддерживаемого прогиба балки», чтобы см. пример расчета на сдвиг сила и изгибающие моменты.Рассчитать сдвиг сил и изгибающих моментов с помощью калькулятора напряжения и прогиба простой опоры балки, как описано в примере. Максимальные усилия сдвига и изгибающие моменты через деревянную балку приведены ниже.
| СДВИГАТЕЛЬНЫЕ СИЛЫ И ИЗГИБЫЕ МОМЕНТЫ | ||
| Расстояние x | Сдвигающая сила (N) | Изгибающий момент (Нм) |
| 0.5 | 12676,5 | 6323 |
| 1,5 | 2500 | 8882 |
Шаг 3. Посетите страницу «Расчет прямоугольной балки на прочность», чтобы рассчитать максимальный сдвиг. и нормальные стрессы.
См. Пример расчета ниже для первой точки, указанной на шаге 2.
| ВХОДНЫЕ ПАРАМЕТРЫ | ||
| Параметр | Значение | |
| Высота несущей балки [2c] | 200 | мм |
| Ширина несущей балки [b] | 100 | |
| Высота y [y] | 100 | |
| Сила сдвига [В] | 12676. 4 | |
| Нормальное напряжение в точке y [σ x ] | 9.484 | МПа |
| Напряжение сдвига в точке y [τ xy ] | 0 | |
| Напряжение фон Мизеса в точке y [σ v ] | 9,484 | |
| Максимальное нормальное напряжение [σ макс ] | 9.484 | |
| Максимальное напряжение сдвига [τ макс ] | 0,951 | |
| Максимальное напряжение по Мизесу [σ v_max ] | 9,484 | |
Шаг 4: Результаты расчета напряжений приведены в следующей таблице.
| РЕЗУЛЬТАТЫ | ||||
| Расстояние x | Сдвигающая сила (N) | Изгибающий момент (Нм) | Максимум.Нормальный Напряжение (МПа) | Максимум. Сдвиг Напряжение (МПа) |
| 0,5 | 12676,5 | 6323 | 9,484 | 0,951 |
| 1.5 | 2500 | 8882 | 13,323 | 0,188 |
Резюме
По результатам дизайн не безопасен для заданных параметров и условий. Максимальное нормальное напряжение (13,323 МПа) превышает допустимое значение (10 МПа), указанное в задаче.Для надежной конструкции следует выбрать деревянную балку большего размера.
Проблема полностью решена с помощью калькуляторов и примеров, которые представлены в виде следует.
Пример отклонения балки с простой опорой
Деревянная балка AB пролетом 3 м, шириной 200 мм и высотой 100 мм предназначена для поддержки трех сосредоточенные нагрузки показаны на рисунке. Модуль упругости выбранного класса древесины составляет 8 ГПа, а плотность бруса 600 кг / м 3
Рассчитайте макс.прогиб, макс. усилие сдвига, макс. изгибающий момент, средний пролет силы прогиба / наклона и конечной реакции деревянной прямоугольной балки для следующих условия загрузки.
Решение:
Шаг 1: Запишите входные параметры (включая свойства материала), которые определено в образце примера.
| ВХОДНЫЕ СВОЙСТВА | ||
| Параметр | Значение | |
| Ширина бруса [b] | 100 | мм |
| Высота бруса [H] | 200 | мм |
| Длина бруса [L] | 3000 | мм |
| Расстояние x (средний пролет) [x] | 1500 | мм |
| Модуль упругости древесины [E] | 8 | ГПа |
| Тип балки | Балка с простой опорой с множественными точечными нагрузками | |
Шаг 2: Перейдите к «Калькулятору свойств сечения твердого прямоугольного стержня» страница для расчета второго момента площади вокруг оси x (I xx )
| ВХОДНЫЕ ПАРАМЕТРЫ | ||
| Параметр | Значение | |
| Высота [H] | 200 | мм |
| Ширина [B] | 100 | |
| Длина [L] | 3000 | |
| Плотность [p] | 600 | кг / м 3 |
| ВЫХОДНЫЕ ПАРАМЕТРЫ | ||
| Параметр | Значение | |
| Площадь поперечного сечения [A] | 20000 | мм ^ 2 |
| Масса [М] | 36 | кг |
| Второй момент площади [I xx ] | 66666668 | мм ^ 4 |
| Второй момент площади [I yy ] | 16666667 | |
| Модуль упругости [S xx ] | 666666.3 | |
| Модуль упругости сечения [S yy ] | 333333.344 | |
| Радиус вращения [r x ] | 57,735 | мм |
| Радиус вращения [r y ] | 28.868 | |
| Расстояние CoG в направлении x [x cog ] | 50 | мм |
| Расстояние CoG в направлении y [y cog ] | 100 | |
Шаг 3: Перейдите на страницу «Калькулятор напряжения и прогиба простой опоры балки», чтобы рассчитать максимальный сдвиг. сила, изгибающий момент и прогиб древесины.Введите три точечные нагрузки, указанные на рисунке, и одну распределенную нагрузку (из-за нагрузки на деревянную балку). собственный вес). Распределенная нагрузка равна (М * г) / L = 36 * 9,81 / 3 = 117,7 Н / м.
На деревянную балку не действует момент, поэтому установите значения момента на 0.
| ВХОДНЫЕ ПАРАМЕТРЫ | |||||||
| ТОЧЕЧНЫЕ НАГРУЗКИ | |||||||
| Параметр | Символ | Величина | Расстояние | ||||
| кН | м | ||||||
| Нагрузка 1 ** | П 1 | 10 | 0.5 | ||||
| Нагрузка 2 ** | П 2 | 5 | 1,5 | ||||
| Нагрузка 3 ** | П 3 | 10 | 2.5 | ||||
| Нагрузка 4 ** | П 4 | 0 | 0 | ||||
| Нагрузка 5 ** | П 5 | 0 | 0 | ||||
| КОНЦЕНТРИРОВАННЫЕ МОМЕНТЫ | |||||||
| Параметр | Символ | Величина | Расстояние | ||||
| Н * м | м | ||||||
| Момент 1 ** | П 1 | 0 | 0 | ||||
| Момент 2 ** | П 2 | 0 | 0 | ||||
| Момент 3 ** | П 3 | 0 | 0 | ||||
| Момент 4 ** | M 4 | 0 | 0 | ||||
| Момент 5 ** | П 5 | 0 | 0 | ||||
| РАСПРЕДЕЛЕННЫЕ НАГРУЗКИ | |||||||
| Параметр | Символ | Величина | Расстояние | ||||
| Н / м | м | ||||||
| wa | wb | b | |||||
| Распределенная нагрузка 1 ** | ш 1 | 117.7 | 117,7 | 0 | 3 | ||
| Распределенная нагрузка 2 ** | ш 2 | 0 | 0 | 0 | 0 | ||
| Распределенная нагрузка 3 ** | ш 3 | 0 | 0 | 0 | 0 | ||
| Распределенная нагрузка 4 ** | ш 4 | 0 | 0 | 0 | 0 | ||
| Распределенная нагрузка 5 ** | ш 5 | 0 | 0 | 0 | 0 | ||
| КОНСТРУКЦИОННАЯ БАЛКА | |||||||
| Параметр | Символ | Значение | |||||
| Длина луча | L | 3 | м | ||||
| Расстояние x | х | 1.5 | |||||
| Модуль упругости | E | 8 | ГПа | ||||
| Расстояние от нейтральной оси до крайних волокон | в | 50 | мм | ||||
| Второй момент области | I | 66666668 | мм ^ 4 | ||||
Шаг 4: Результаты вычислений на шаге 3 следующие.
| ВХОДНАЯ НАГРУЗКА НА ПРОСТО ОПОРНУЮ БАЛКУ | ||||||||||||||
| ТОЧЕЧНЫЕ НАГРУЗКИ | ||||||||||||||
| ||||||||||||||
| КОНЦЕНТРИРОВАННЫЕ МОМЕНТЫ | ||||||||||||||
| РАСПРЕДЕЛЕННЫЕ НАГРУЗКИ | ||||||||||||||
| ||||||||||||||
| РЕЗУЛЬТАТЫ | ||||||||||||||
| Параметр | Значение | |||||||||||||
| Сила реакции 1 [R 1 ] | 12676.5 | N | ||||||||||||
| Сила реакции 2 [R 2 ] | 12676,5 | |||||||||||||
| Поперечное поперечное усилие на расстоянии x [V x ] | 2500,0 | |||||||||||||
| Максимальная поперечная поперечная сила сдвига [V max ] | 12676.5 | |||||||||||||
| Момент на расстоянии x [M x ] | 8882,4 | Н * м | ||||||||||||
| Максимальный момент [M max ] | 8882,4 | |||||||||||||
| Наклон 1 [θ 1 ] | -0.988 | степень | ||||||||||||
| Наклон 2 [θ 2 ] | 0,988 | |||||||||||||
| Наклон на расстоянии x [θ x ] | 0,000 | |||||||||||||
| Максимальный наклон [θ макс ] | -0.988 | |||||||||||||
| Прогиб на расстоянии x [y x ] | -15,662 | мм | ||||||||||||
| Максимальный прогиб [y max ] | -15,662 | |||||||||||||
| Напряжение изгиба на расстоянии x [σ x ] | 6.7 | МПа | ||||||||||||
| Максимальное напряжение изгиба [σ макс ] | 6,7 | |||||||||||||
Сводка
Макс. прогиб, макс. усилие сдвига, макс. изгибающий момент, прогиб / наклон в середине пролета и силы реакции конца деревянной прямоугольной балки были рассчитаны с помощью использование следующих калькуляторов.




 При дальнейшем росте изгибающего момента пластические деформации растут и происходит разрушение в результате разрыва крайних растянутых волокон. Максимальный относительный прогиб балок и прогонов покрытий не должен превышать 1/200.
При дальнейшем росте изгибающего момента пластические деформации растут и происходит разрушение в результате разрыва крайних растянутых волокон. Максимальный относительный прогиб балок и прогонов покрытий не должен превышать 1/200.